莉丝前端

递归的定义

根据wiki百科，递归（英语：Recursion），又译为递回，在数学与计算机科学中，是指在函数的定义中使用函数自身的方法。递归的能力在于用有限的语句来定义对象的无限集合。一般来说，递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

递归的实现机制

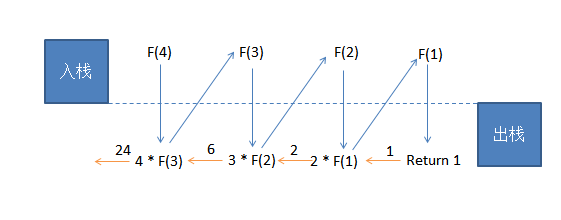
在一些编程语言里，递归机制的实现数据模型是堆栈，即后进先出的数据结构。下图展示了递归的调用栈，一次递归可以分解为入栈及出栈两步，蓝色箭头线展示了入栈的过程，直到达到退出条件，则转为红色线表示的出栈过程，并一步步推算得出结果。

简单的递归（求阶乘）

一些问题，可以轻易的写出递归，比如求阶乘

public int f(int n){  
    if(n < 2 ){    
        return n;
  }else{    
      return n * f(n - 1);
  }
}

组合使用递归

更多的问题，使用无法使用单个递归解决，而是要组合使用递归思想，比如递归求简单交错幂级数的部分和：

public double sum(double x, int n){  
  if(n == 1){    
        return x;
  }else{  
      return mult(x , n) + sum(x , n - 1);
  }
}
public double mult(double x , int n){  
  if(n == 1 ){    
      return x;
  }else{    
      return (-1) * x * mult(x , n - 1);
  }
}

上述代码中，sum()方法作为递归方法，调用了另外一个递归方法mult()，通过递归的嵌套组合使用，来完成简单交错幂级数的部分和计算。

递归的特点

1、是处理逻辑的抽象，抽象程度高，能解决常规方法所不能解决的问题。

2、内存消耗大、计算成本高，由于要在内存里记录每一层返回点和局部变量。它的计算规模和能力取决于内存和cpu的能力。